
乗っていた飛行機が乱気流に巻き込まれ、思わず叫び声をあげたことはないだろうか。このとき、隣に座っていた乗客が、「ちょっと計算してみたんですが、この飛行機が墜落する確率は0.001%以下で、無視してかまいませんよ」といったら、あなたは「世界を支配する秘密結社」のメンバーの一人にたまたま出会ったことになる。
秘密結社といっても、フリーメーソンやイルミナティ、ディープステイトのことではない。こんなとき、次の頁の数式を頭に浮かべている者たちのことだ。
これはベイズの定理で、ある状況が変化したとき、確率がどのように更新されるかを表わしている。
Pは確率(Probability)の頭文字で、P(M|D)は「飛行機がひどく揺れていると仮定した場合の墜落の確率」。それを計算するには「なにも起きていない段階で、飛行機が墜落する統計的確率(1000万分の1)」「墜落する前にひどい揺れが起きる確率(これは間違いないので確率1=100%)」「無事に着陸できるのにひどく揺れる確率(このような統計はすぐに手に入らないので、主観的に100分の1とする)」があればいい。これをベイズの数式にあてはめると、この飛行機が墜落する確率が10万分の1で、無事に着陸できる確率が99.999%であることがわかる。※1
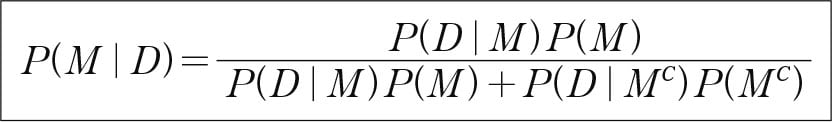
ベイズの定理がいっていることは、直観的にも説明できる。「統計的にものすごく低い確率でしか起こらないこと(飛行機の墜落)に、なんらかの要因(乱気流)が加わって確率がすこし上がったとしても、ヒドいこと(墜落)はやっぱりものすごく低い確率でしか起こらない」のだ。
ここまでは凡人でも理解できるだろうが、世の中にはこのようなとき、ごく自然にベイズの数式を呼び出し、それに数字をあてはめて計算し、どのように判断・行動するかを決めるひとがいる。それが「世界を数学的に把握する者たち」であり、本書の主人公である「テクノ・リバタリアン」だ。




























